道格拉斯-普克算法(Douglas–Peucker algorithm),亦称为拉默-道格拉斯-普克算法(Ramer–Douglas–Peucker algorithm),这个算法最初由拉默(Urs Ramer)于1972年提出,1973年道格拉斯(David Douglas)和普克(Thomas Peucker)二人又独立于拉默提出了该算法。
在计算机当中,曲线可以用足够多的点来描述,那么如何用尽可能少的点来描述这条曲线呢,这就是该算法要实现的目标,同时因为用来描述曲线的点变少了,也可以认为其对数据进行了压缩,减少了数据量。
算法流程
- 首先明确程序的输入是一系列的点构成的曲线,输出的是其中一部分点构成的曲线;
- 将曲线首尾AB两点连成一条直线(程序中应当是理论计算出);
- 然后分别计算曲线上各点到这条直线的距离,并取出其中的最远距离与阈值进行比较(该阈值通常人为确定);
- 若是大于阈值,则保留该最大距离对应的点C,此时可以生成两条直线AC、CB,重复步骤三;
- 若是小于阈值,则算法结束。
算法实现
代码非本人原创,我只是个代码的搬运工
import math
import re
import matplotlib.pyplot as plt
def DPeucker(dataOrigin, epsilon=0.6):
data = list()
# to make sure that the datatype is list type instead of numpy list
# print(type(dataOrigin))
if(type(dataOrigin) == type([])):
print("the type is right")
else:
for i in range(dataOrigin.shape[0]):
data.append(list(dataOrigin[i]))
# print(data)
removeLabel = list()
label_init = lineSegments(data, 0, len(data), removeLabel, epsilon)
# from bigger to smaller to remove the redundant data, sort it and remove the repeat data.
labelFinal = list()
label_init.sort(reverse=True)
for item in label_init:
if not item in labelFinal:
labelFinal.append(item)
# remove the redundant point
for i in range(len(labelFinal)):
del data[labelFinal[i]]
# get the point
# print(data)
if(type(dataOrigin) == type(np.array(0))):
data = np.array(data)
return data
def calLinePara(start, end):
# input parameters is two end points
if(end[0] - start[0] != 0):
k = (end[1] - start[1]) / (end[0] - start[0])
b = (end[0] * start[1] - end[1] * start[0]) / (end[0] - start[0])
if(end[1] - start[1] != 0):
x_axis = -b / k
else:
x_axis = None
else:
k = None
b = None # mean the paras is inexistence.
x_axis = end[0]
return (k, b, x_axis)
# figure out the distance from dot to line
def dotToLIneDistance(point, k, b, a_axis):
if k == None and b == None:
distance = abs(a_axis - point[0])
else:
distance = abs(k * point[0] - point[1] + b) / math.sqrt(k * k + 1)
return distance
# recall itself to finish segments itself
def lineSegments(listData, startLabel, endLabel, removeLabel, epsilon):
# removeLabel is a list as a formal parameter, and will be changed by the function
if((endLabel - startLabel) <= 1):
return removeLabel
else:
k, b, x_axis = calLinePara(listData[startLabel], listData[endLabel-1])
distance = list()
for i in range(startLabel+1, endLabel):
# print(dotToLIneDistance(listData[i], k, b, x_axis))
distance.append(dotToLIneDistance(listData[i], k, b, x_axis))
# print(distance)
# print(max(distance))
if(max(distance) <= epsilon):
# print(endLabel-1, startLabel)
for i in range(startLabel+1, endLabel):
# for i in range(endLabel-1,-1, int(startLabel)):
removeLabel.append(i)
else:
middleLabel = distance.index(max(distance)) + startLabel + 1
lineSegments(listData, middleLabel, endLabel, removeLabel, epsilon)
lineSegments(listData, startLabel,
middleLabel, removeLabel, epsilon)
return removeLabel
算法demo
其中部分函数为自己编写,并不作为通用范例,仅展示函数调用及使用方法
import math
import re
import sys
from pathlib import Path
# use the dp algorithm to simplify the line.
current_folder = Path(__file__).absolute().parent
father_folder = str(current_folder.parent)
sys.path.append(father_folder)
import matplotlib.pyplot as plt
import numpy as np
from package.func import *
if __name__ == "__main__":
filepath = r"14_15.txt"
x, z = load_txt(filepath)
show_pic(x, z)
# 数据拼接
dataList = np.c_[x, z]
dataFinal = DPeucker(dataList, epsilon=0.6)
x_out = np.array(dataFinal)[:, 0]
z_out = np.array(dataFinal)[:, 1]
show_pic(x_out, z_out)
实现结果
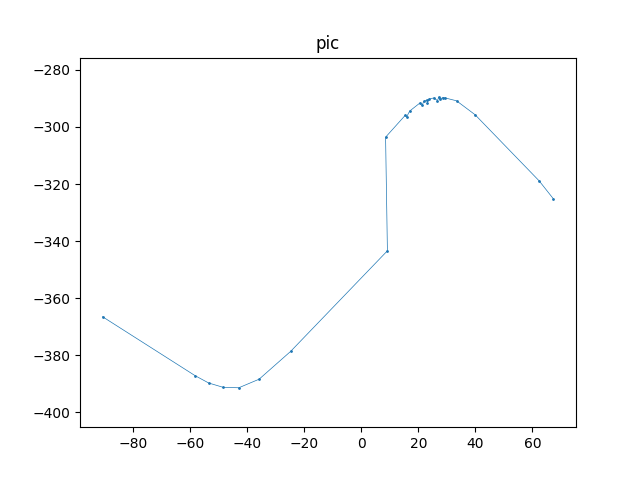
原始数据:

经过处理后数据: