回归问题
假定我们现有一大批数据,包含房屋的面积和对应面积的房价信息,如果我们能得到房屋面积与房屋价格间的关系,那么,给定一个房屋时,我们只要知道其面积,就能大致推测出其价格了。
所以,回归问题的特点是:回归问题通常是用来预测一个值,且预测的结果是连续的。
一个比较常见的回归算法是线性回归算法(Linear Regression)(LR)
一个预测问题在回归模型下的解决步骤为:
-
积累知识: 我们将储备的知识称之为训练集(Training Set),很好理解,知识能够训练人进步。
-
学习:学习如何预测,得到输入与输出的关系。在学习阶段,应当有合适的指导方针,江山不能仅凭热血就攻下。在这里,合适的指导方针我们称之为学习算法(Learning Algorithm)
-
预测:学习完成后,当接受了新的数据(输入)后,我们就能通过学习阶段获得的对应关系来预测输出。
学习过程往往是艰苦的,“人谁无过,过而能改,善莫大焉”,因此对我们有这两点要求:
- 有手段能评估我们的学习正确性。
- 当学习效果不佳时,有手段能纠正我们的学习策略。
线性回归
问题阐述
假设现在我们遇到一个实际问题:现在我们有一堆数据,分别包含房屋的面积和对应面积的房价信息,要求我们当我们得到一个新的房屋面积时,预测房子的价格。这里我们将问题简化为单变量问题来看
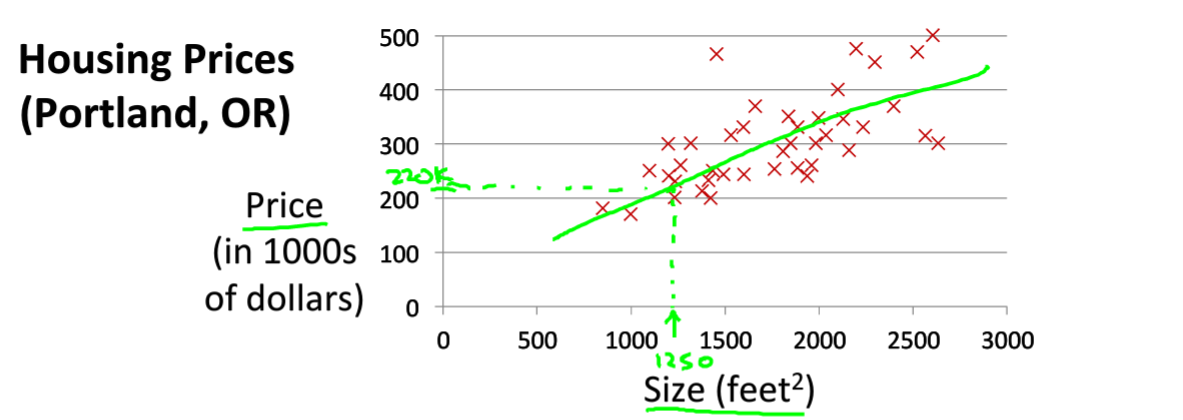
回归过程
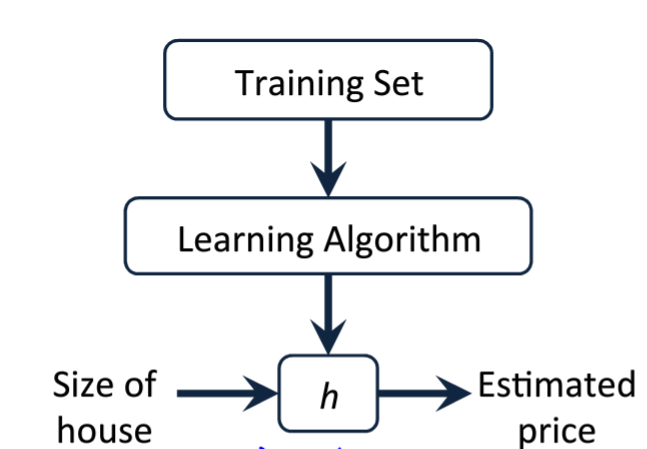
将训练集放入学习算法当中进行训练,为假设函数 $h(x)$ 找出最适合的参数,当放入一个训练集之外的数据时,函数给出预测。
符号定义
- 特征(feature):$x$ , 房屋的面积
- 特征向量(输入): $x^i$ ,$i$用来描述第几套房子
- 样本数:m,用来描述数据量的多少
- 目标变量:y,
- 参数(Parameters):$\theta_i$